Universal Scalability for Orgs

January 20, 2020. Tags [ scalability, management, organization, USL ]

Last week, Coda Hale published a very thought-provoking essay, “Work is Work” where he explores what is necessary to increase (not to mention just maintain) productivity as an organization increases in size. A man after my own heart, he applies queuing theory to the process of getting work done in increasingly larger organizations.

I was inspired to look at the same problem through a slightly different theoretic lens: the Universal Scalability Law (USL), as put forth by Neil Gunther. I first encountered this concept his his excellent book Guerilla Capacity Planning. It gives a way to reason about the relative speedup you can get from adding processing units (whether these are CPUs, server instances, or staff). The USL says:

C(N)

1 + α(N − 1) + βN(N − 1)

Here, C(N) is the relative speedup from having N workers as compared to just one worker: if C(N) is 2, then you have twice the total throughput with N workers than you did with one. There are then two coefficients that drive the rest of the equation:

α: a measure of the degree of contention for shared resources
β: a measure of the overhead due to the need for coherence between workers (i.e. coordination, keeping everyone up-to-date, etc.)

If both α and β are zero, then we get straight linear scaling:

C(N)

If β is zero, then we are essentially limited just by contention for shared resources (i.e. the non-parallelizable work), which astute readers will recognize as Amdahl’s Law:

C(N)

1 + α(N − 1)

The coherence term (with β) is really the interesting contribution Gunther makes here, because it brings an N² overhead to scaling. Where Amdahl’s law by itself brings us diminishing returns as we add more workers, the full USL models situations where adding more workers makes us slower! Consider this graph where we have set α=0.01 and β=0.02:

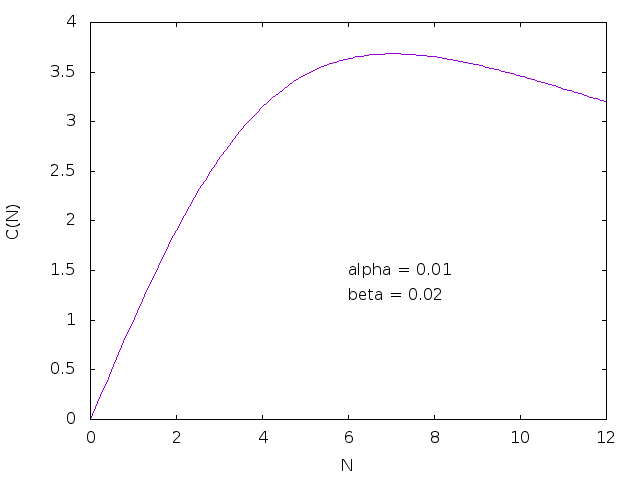
We can see that once N exceeds something right around 7, total throughput starts declining. Perhaps there is something to Fred Brooks’ observation that “adding [people] to a late software project makes it later.” Incidentally, this raises an interesting side question: given the empirical optimal Scrum team size of 7±2, two-pizza teams, optimal meeting sizes under 8 people, etc.: is the natural coefficient of coherence for a team of humans somewhere around 0.02? If so, what would we do with this information?

I wonder if this is what gives rise to Conway’s Law: once you have a sufficiently large number of humans trying to work together, in order to make forward progress, you need to limit the N² overheads and so you have to start thinking and treating co-teams/subcommittees as single entities to communicate with. As my uncle, a retired professor of anthropology, told me once: the single thing holding back human society is that we each have only 1400 cubic centimeters of brain.

Indeed, we can see that traditional tree-structured organizational hierarchies can be attractive in terms of simplifying communication paths and allowing for the encapsulation/abstraction of “subtrees” of the overall organization, at the expense of potentially higher coherence overheads when the organization is not designed properly, as in the study from Microsoft that showed that organizational distance of collaborators was a good predictor for bugginess of code!

Implications for Organizations

Scaling effectively thus boils down to reducing either contention on shared resources (α) or reducing coherence/communication overheads (β). Examples of the former we’ve seen recently include cross-functional teams that are responsible for their own testing and deployments (breaking a dependency on a shared bottleneck QA or TechOps organization). Examples of the latter can include the adoption of microservices or, arguably, the use of Objectives and Key Results (OKRs) as an attempt at a lower communication mechanism for achieving alignment.

This also shows us things aren’t always simple, either: while breaking functionality up across microservices might create smaller teams with lower coherence overheads, I can easily create contention at the same time. If I don’t factor out my microservices carefully, I can end up in situations where I need to coordinate across multiple teams just to ship a single end-to-end feature.